피타고라스정리 - 닮은 삼각형으로 증명
- 삶/눈높이공부
- 2021. 7. 7.
여러 삼각형의 닮은꼴을 사용하여 피타고라스정리를 유도하는 방법에 대해 살펴보겠습니다.
우선 다음과 같은 직각 삼각형으로부터 시작해 보죠.

직각의 꼭지점으로부터 수선의 발을 내려봅시다.

그러면, 이 안에서 서로 닮은 삼각형들을 찾을 수 있습니다. 삼각형의 내각의 합이 180도라는 점을 활용하여, 다음과 같이 같은 각도들을 표시할 수 있습니다.
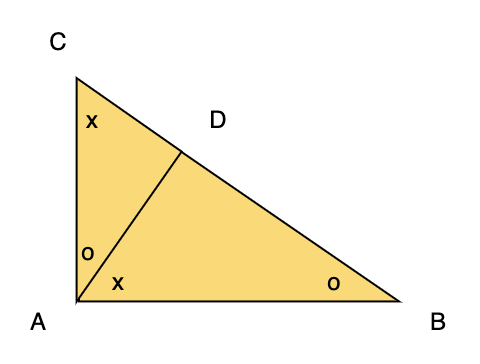
삼각형의 변의 길이를 아래와 같이 표시해 봅니다.

이 삼각형들을 분리하고, 회전시켜 재배치 하면 아래 그림과 같이 볼 수 있습니다.

이제 비례식을 세워봅시다. 만약, 1:2 = 2:4 라는 비례식이 성립한다면 $ 1 \times 4 = 2 \times 2 $ 와 같이 식을 수립할 수 있을 것입니다.
$ a:b = d:c2 = c1:d $
$ a:c1+c2 = d:b = c1:a $
$ b:c1+c2 = c2:b = d:a $
위의 식들로부터, 여러가지 조합을 만들 수 있지만, 피타고라스 정리와 비슷한 조합 위주로 추려 봅시다.
$ a \times a = c1 \times (c1 + c2) $
$ b \times b = c2 \times (c1 + c2) $
위의 두 식을 좌변과 우변을 각각 더하면,
$ a^2 + b^2 = c1 \times (c1 + c2) + c2 \times (c1 + c2) $
그런데, c는 원래 한 변을 뜻하기에 c = c1 + c2 라고 할 수 있으므로 위의 식은 다음과 같이 다시 쓸 수 있습니다.
$ a^2 + b^2 = c1 \times c + c2 \times c = (c1 + c2) \times c = c \times c = c^2 $
$ a^2 + b^2 = c^2 $
삼각형의 닮음 꼴들로부터, 피타고라스 정리를 유도하였습니다.
'삶 > 눈높이공부' 카테고리의 다른 글
| 원기둥 부피 공식 이해하기 (0) | 2023.02.18 |
|---|---|
| 원의 둘레 공식, 원의 넓이 공식 이해하기 (0) | 2023.01.16 |
| 두 분수에 곱해서 자연수를 만들 수 있는 가장 작은 분수 구하기 (0) | 2022.05.16 |
| 근의 공식 유도 (0) | 2021.07.22 |
| 피타고라스 정리 - 유클리드 증명 (0) | 2021.06.30 |
| 피타고라스 정리 - 가필드식 증명 (0) | 2021.06.23 |
| 피타고라스 정리 - 바스카라식 증명 (0) | 2021.06.16 |
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |