피타고라스 정리 - 바스카라식 증명
- 삶/눈높이공부
- 2021. 6. 16.
피타고라스 정리 - 바스카라식 증명
피타고라스 정리 증명 방법만으로도 약 400여가지 이상이 있다고 하는데, 오늘은 인도수학자 바스카라식 증명 방법을 정리합니다.
지난 번 피타고라스식 증명과 마찬가지로 도형을 나누고, 전체 넓이 = 부분 넓이의 합 방식으로 증명하는 방식입니다.
중학 수학 과정에서 모든 방법을 다 알 필요는 없겠지만, 응용 문제를 준비하는 관점에서도 봐두면 좋을 것 같습니다.
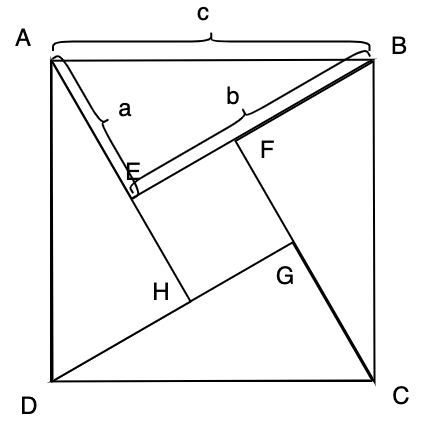
정사각형 ABCD를 기준으로, 대각선이 c가 되는 직각 삼각형을 그려봅니다.
그러면 삼각형 ABE와 같은 모양이 됩니다. 그리고, 각 모서리를 기준으로 돌려가면서 배치하면, 가운데 정사각형 EFGH를 남겨놓는 모양이 됩니다.
이제 넓이를 비교해 봅시다.
- S1 = 전체 정사각형(ABCD)의 넓이 = $ c * c = c^2 $
- S2 = 부분 도형들의 넓이의 합 = 삼각형 ABE + 삼각형 BCF + 삼각형 GCD + 삼각형 AHD + 정사각형 EFGH = $ 4 \times \frac 1 2 \times a \times b + (b - a)^2 $
S1 = S2 이므로,
$ c^2 = 2ab + b^2 - 2ab + a^2 $
$ c^2 = a^2 + b^2 $
$ a^2 + b^2 = c^2 $
이상으로, 중2 수학 피타고라스 정리를 바스카라 방식으로 증명했습니다.
'삶 > 눈높이공부' 카테고리의 다른 글
| 근의 공식 유도 (0) | 2021.07.22 |
|---|---|
| 피타고라스정리 - 닮은 삼각형으로 증명 (0) | 2021.07.07 |
| 피타고라스 정리 - 유클리드 증명 (0) | 2021.06.30 |
| 피타고라스 정리 - 가필드식 증명 (0) | 2021.06.23 |
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |
| 초보자도 이해하기 쉬운 대우명제 (1) | 2021.04.12 |
| 최대공약수와 최소공배수 활용 (1) | 2021.02.10 |
| 최소공배수 구하는 법 - 여러가지 방법 비교 (0) | 2021.02.05 |