피타고라스 정리 - 유클리드 증명
- 삶/눈높이공부
- 2021. 6. 30.
피타고라스 정리 - 유클리드 증명
중학 수학에 소개되는 피타고라스정리를 유클리드 증명으로 도출해 봅시다.
유클리드 증명은 아래와 같이 세 개의 정사각형을 기대어 놓은 형태로부터 출발합니다.

한 변의 길이가 각각 a, b, c인 세 개의 정사각형이 표시되어 있습니다.
위의 두의 정사각형의 넓이의 합은 아래 큰 정사각형의 넓이와 같다는 것을 통해 증명하는 방법입니다.

원래는 정사각형들만 있는 그림에, 위와 같이 대각선들을 이어서 내부에 몇 개의 삼각형을 그립니다.
$ \triangle BCD $ 와 $ \triangle BCG $를 볼까요?

두 삼각형은 밑변과 높이가 각각 a로 동일하기 때문에 넓이가 같습니다.
이번에는 $ \triangle BCG $ 와 $ \triangle CED $를 비교해 볼까요?

$ \overline {BC} = \overline {CD} $ 이고, $ \overline{CG} = \overline{CE}$ 입니다.
$ \angle{BCD} = \angle{ECG} = 90 ^{\circ} $ 이고, $ \angle {DCG} $는 공통이므로, 두 삼각형은 같은 삼각형입니다.
즉, 회전시킨 삼각형이라 볼 수 있습니다.
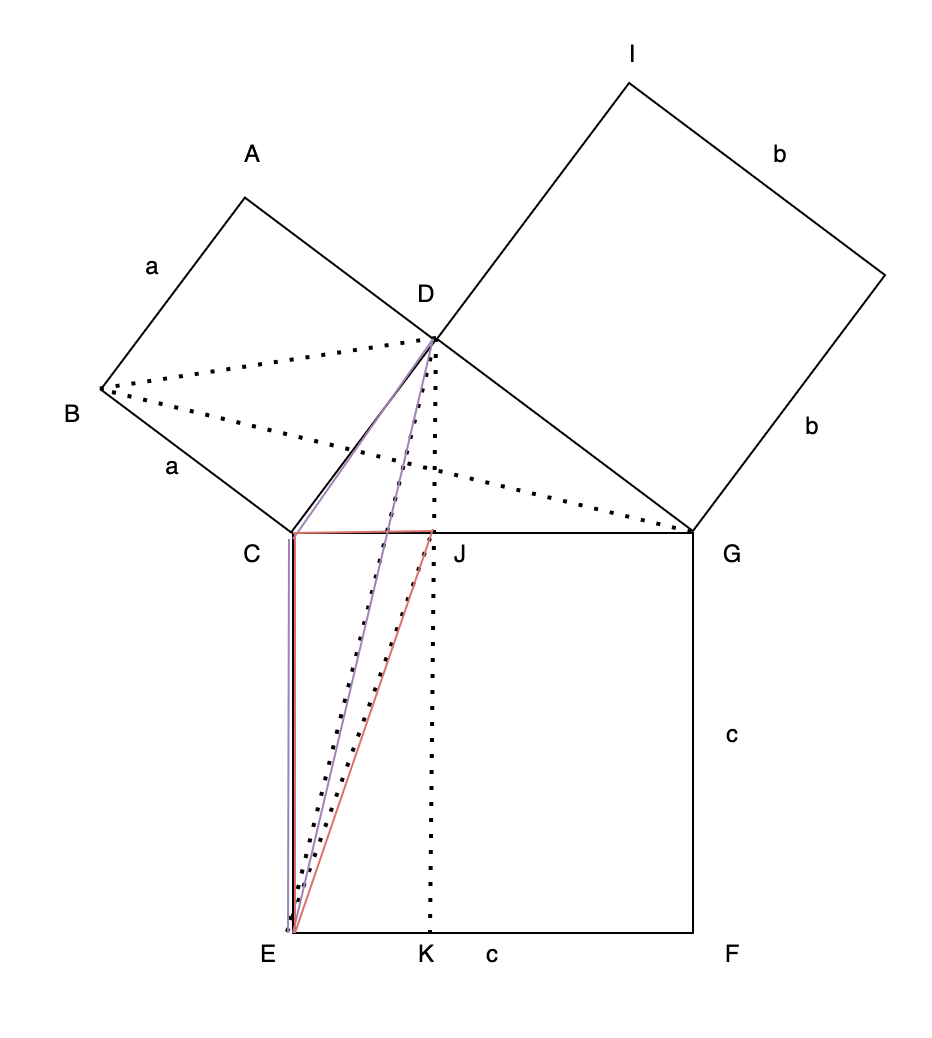
위와 같은 원리로 $ \triangle {CED} $와 $ \triangle {CEJ} $ 는 넓이가 같은 삼각형입니다.
여기까지의 내용으로, $ \triangle {BCD} $의 넓이는 $ \triangle {CEJ} $의 넓이와 같다는 것을 확인했습니다.
사각형을 반으로 나눠 검증을 했으니, 나머지 반쪽도 마찬가지일 것입니다.
옮겨오지 않은 나머지 삼각형은 앞서 구한 삼각형 넓이의 각각 두 배를 한 것과 같을 것입니다.
즉, $ \square {ABCD}$ 의 넓이 = $ \square{CEKJ} $의 넓이입니다.
같은 방법으로 오른쪽 사각형에 대해서도 검증을 해볼 수 있겠죠?
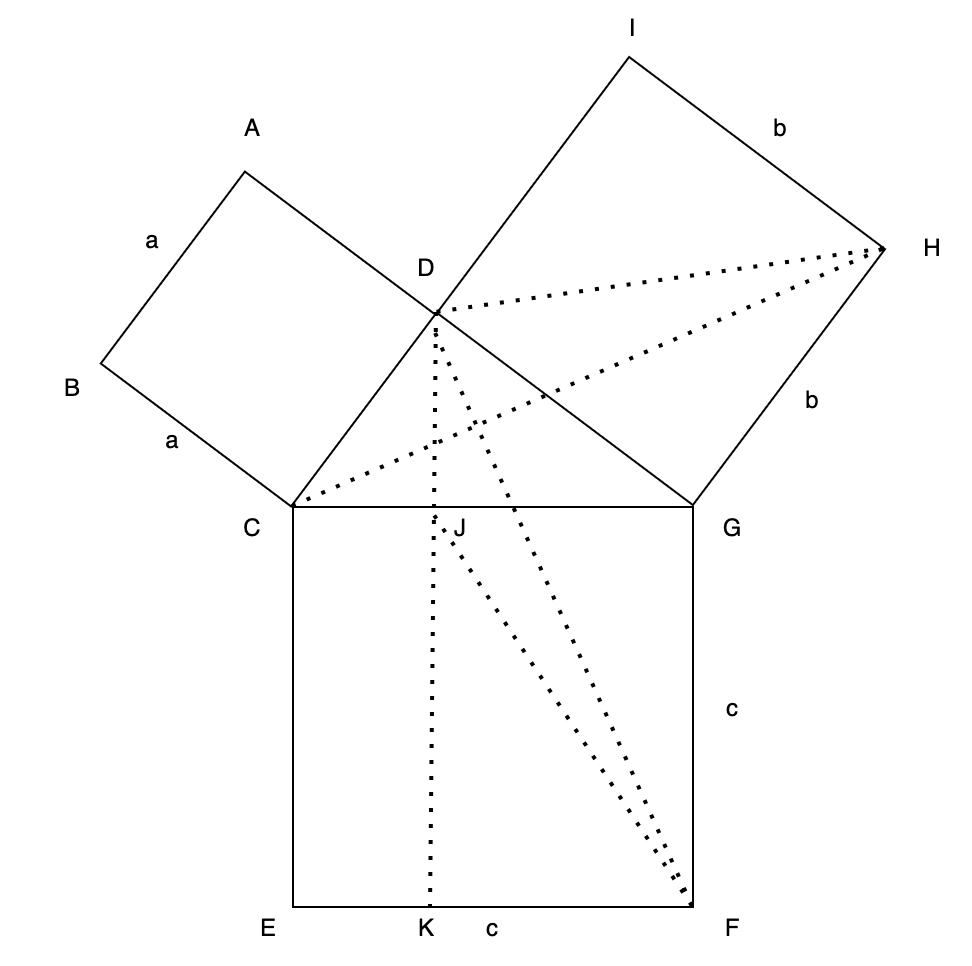
$ \triangle {GHD} $ 와 $ \triangle {FGJ} $의 넓이는 같고, $ \square {DGHI}$ 와 $ \square {FGJK}$의 넓이 또한 같게 됩니다.
지금까지 한 검증 결과를 모으면, 다음과 같이 될 것입니다.
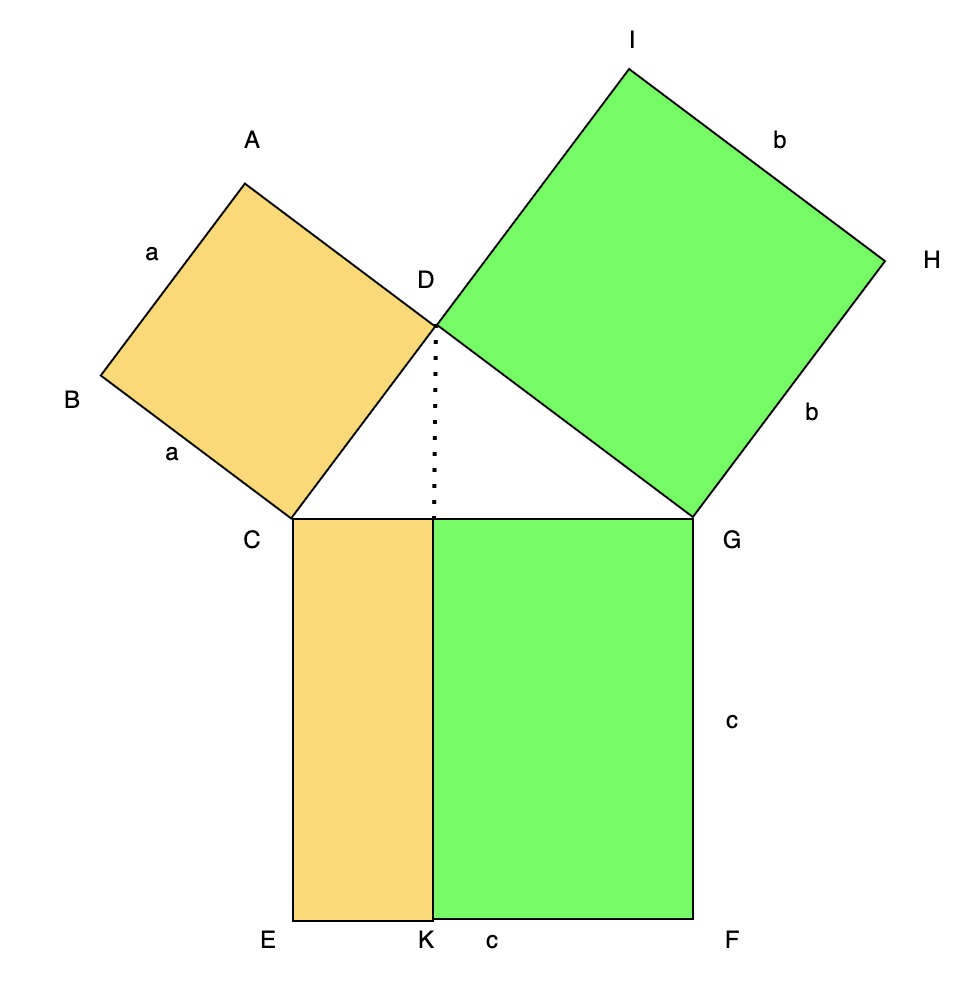
따라서, 위의 두 정사각형의 넓이의 합은 아래 큰 정사각형의 넓이의 합이 된다는 것을 확인할 수 있습니다.
$ \square {ABCD} + \square {DGHI} = \square {CEFG} $
따라서, $ a^2 + b^2 = c^2 $
위와 같이 중2 수학 피타고라스의 정리를 유클리드 방식으로 증명하였습니다.
'삶 > 눈높이공부' 카테고리의 다른 글
| 원의 둘레 공식, 원의 넓이 공식 이해하기 (0) | 2023.01.16 |
|---|---|
| 두 분수에 곱해서 자연수를 만들 수 있는 가장 작은 분수 구하기 (0) | 2022.05.16 |
| 근의 공식 유도 (0) | 2021.07.22 |
| 피타고라스정리 - 닮은 삼각형으로 증명 (0) | 2021.07.07 |
| 피타고라스 정리 - 가필드식 증명 (0) | 2021.06.23 |
| 피타고라스 정리 - 바스카라식 증명 (0) | 2021.06.16 |
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |
| 초보자도 이해하기 쉬운 대우명제 (1) | 2021.04.12 |