초보자도 이해하기 쉬운 대우명제
- 삶/눈높이공부
- 2021. 4. 12.
초보자도 이해하기 쉬운 대우명제
시간이 한참 지나니, 논리학의 어떤 명제와 그 대우명제가 같은 진리값을 지닌다는 사실만 기억에 남고, 왜 그러한지는 설명하기 어렵더군요. 그래서, 이번 기회에 정리하고자 합니다.
논리 명제(proposition)의 일반적인 표기
- $ p $ : p
- $ \neg q $: q가 아님 (negation)
- $ p \rightarrow q $ : p이면 q이다.
- $ p \rightarrow \neg q $ : p이면 q가 아니다.
명제의 논리 유형
원래의 명제가 $ p \rightarrow q $ (p이면 q이다) 라고 주어졌을 때, 위와 같이 표기하는 조건식의 관계의 변형은 다음과 같은 유형으로 나뉩니다.
역(converse)
가정과 결과가 뒤 바뀌는 것을 뜻합니다. $ q \rightarrow p $를 뜻합니다.
이(inverse)
가정과 결과를 각각 부정한 것을 뜻합니다. $ \neg p \rightarrow q $를 뜻합니다.
대우(contrapositive)
가정과 결과를 각각 부정하고, 위치를 서로 바꾸는 것을 뜻합니다. $ \neg q \rightarrow \neg p $를 뜻합니다.
원래의 명제와 역, 이는 진리값이 그대로 보존되는 것을 보장하지 않으나, 대우명제와는 진리값이 같다고 외웠는데 위의 문장을 봐도 잘 와닿지 않습니다. 그래서, 그림과 예제로 이해하는 것이 좋을 것 같습니다.
그림으로 살펴보는 논리 유형
사과와 과일을 예제로 논리 명제를 이해해 봅시다.
- 사과(p)는 과일이다(q).
그런데, 이 문장의 이해를 돕기 위해 다음과 같이 의역해 볼 수 있습니다. - 사과(p)는 과일에 속한다(q).
따라서, 이 명제의 대우 명제와 그 의역은 각각 다음과 같습니다.
- 대우명제) 과일이 아니면, 사과가 아니다. (문장이 어색하기에 한번에 이해하기 어렵군요.)
이 난해한 문장의 이해를 돕기 위해 상황을 가정해 봅니다.
스무 고개를 생각해 볼까요? 과일인지 물어보고, 과일이 맞다면 나중에 여러 과일 중, 단서를 파악한 후 사과인지 물어보려고 합니다.
Q) 과일입니까?
A) 아니오.
과일이 아니라는데, 굳이 사과인지 물어볼 필요가 없어졌습니다. 따라서, 위의 난해한 문장은 "과일도 아니라면, 사과일리도 없다." 와 같이 됩니다. 결국, "사과는 과일이다"의 대우명제는 "과일이 아니라면, 사과도 아니다"가 되고 이 문장들의 진리값은 서로 같게 됩니다.
앞서 말한 설명을 그림으로 옮기면, 다음과 같습니다.
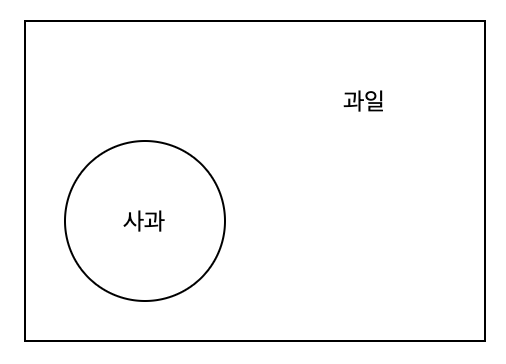
그리고, 이를 p와 q로 일반화 시켜 표현하면 아래와 같습니다.
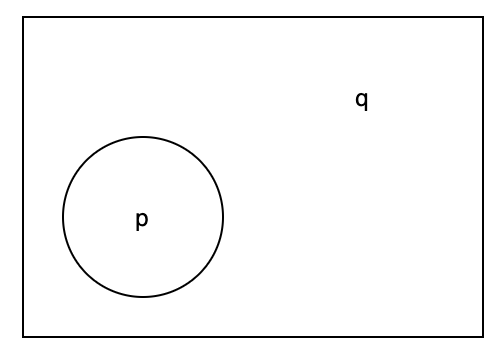
이제 집합의 관점에서 위의 기본 명제와 그 대우명제를 재해석(의역) 해봅시다.
- $ p \rightarrow q $
= p이면 q이다.
= p에 속하면, q에도 속한다. - $ \neg q \rightarrow \neg p $
= q가 아니면, p가 아니다.
= q에 속하지 않으면, p에도 속하지 않는다.
진리표 관점에서 살펴보기
| p | q | $ p \rightarrow q $ | $ q \rightarrow p $ | $ \neg p \rightarrow \neg q $ | $ \neg q \rightarrow \neg p $ |
| 참 | 참 | 참 | 참 | 참 | 참 (거짓 -> 거짓) |
| 참 | 거짓 | 거짓 | 참 | 참 | 거짓 (참 -> 거짓) |
| 거짓 | 참 | 참 | 거짓 | 거짓 | 참 (거짓 -> 참) |
| 거짓 | 거짓 | 참 | 참 | 참 | 참 (거짓 -> 거짓) |
따라서, 어떤 명제의 대우명제는 항상 진리값이 일치하는 것을 확인할 수 있습니다.
'삶 > 눈높이공부' 카테고리의 다른 글
| 피타고라스 정리 - 유클리드 증명 (0) | 2021.06.30 |
|---|---|
| 피타고라스 정리 - 가필드식 증명 (0) | 2021.06.23 |
| 피타고라스 정리 - 바스카라식 증명 (0) | 2021.06.16 |
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |
| 최대공약수와 최소공배수 활용 (1) | 2021.02.10 |
| 최소공배수 구하는 법 - 여러가지 방법 비교 (0) | 2021.02.05 |
| 최대공약수 구하는법 - 여러가지 방법 비교 (3) | 2021.02.03 |
| 서로소, 소수 (prime number) - 다시 생각해 봅시다 (0) | 2021.01.27 |