최대공약수 구하는법 - 여러가지 방법 비교
- 삶/눈높이공부
- 2021. 2. 3.
최대공약수 구하는 법 - 4가지
이번에는 최대공약수 구하는법에 대해서 정리해 보겠습니다. 먼저 최대공약수란 무엇인지부터 살펴봐야겠죠?
요새는 초등학교 5학년 수학 과정에서 다루고 있습니다.
무조건 외우게 하는 것보다, 원리와 배경을 통해 이해하도록 하는 것이 중요합니다.
최대공약수란?
최대공약수는 한자로 最大公約數라고 씁니다.
- 最大: 가장 크다
- 公約數: 공평하게 나눈 수 (똑같이 나눈 수)
즉, 공약수 중 가장 큰 수라는 뜻입니다. 우리 말로 풀어써도 어렵습니다.
한편, 최대공약수를 영어로는 Great Common Divisior 라고 부릅니다.
- Divisior = 나누는 수 = 약수
- Common = 공통의
- Great = 가장 큰
한자로 표기한 최대 공약수와 거의 비슷한 뜻이라 볼 수 있습니다.
오히려, 한자로 표기된 것보다 뜻은 더 이해하기 쉬운 것 같습니다.
공통된 약수들 중 가장 큰 수라고 보면 됩니다.
방법-1
예를 들어, 30과 48의 약수를 각각 나열하면 아래와 같습니다.
- 30 = 1, 2, 3, 5, 6, 10, 15, 30
- 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24,48
이 두 약수 집합중 공약수(common divisor)들은 {1, 2, 3, 6}입니다.
이 중, 가장 큰 숫자는 6입니다.
따라서, 정의에 따라서 30과 48의 최대공약수는 6이 됩니다.
방법-2
각각의 숫자를 소인수분해를 합니다.
$ 30 = 2 \times 3 \times 5 $
$ 48 = 2^4 \times 3 $
소인수 분해를 한 후, 두 수의 공통된 소인수(2와 3) 중 지수가 작은 것들을 곱합니다.
즉, 30에서의 2와, 48에서의 $ 2^3$ 에서 더 작은 지수에 해당되는 2를 택하고, 30과 48에서는 모두 3이므로 3을 택합니다.
이 두 수를 곱하면 최대공약수를 얻을 수 있습니다.
$ 2 \times 3 = 6 $
방법-3
두 수를 공약수로 나눠줍니다.
남는 수가 서로소가 될 때까지 이를 반복합니다.
서로소에 도달하게 되면, 나눠왔던 공약수들을 모두 곱합니다.
이 값이 최대공약수가 됩니다.
2 ) 30 48
3 ) 15 24
5 8
5와 8은 서로소입니다.
두 수의 공약수는 1밖에 없기 때문입니다.
따라서, 이 계산과정에서 사용된 공약수들을 곱하면, $ 2 \times 3 = 6 $ 이 되고, 이 값이 최대공약수가 됩니다.
서로소, 소수 (prime number) - 다시 생각해 봅시다
예전에는 아무 거리낌 없이 받아들이고 그러려니 했던 말 중에 서로소라고 있습니다. 이것을 설명하려니 왜 탁 막힐까요? 아마, 당시에 나의 언어로 소화하는 과정을 잘 거치지 않았던 모양입니
luran.me
방법-4
유클리드 호제법으로 풀어봅시다.
유클리드 호제법이란 이름만으로만 보자면 다음과 같습니다.
- 유클리드라는 사람이 만든
- 호제법: 서로 나누는 방법
최대공약수(Great Common Divisor)를 구하는 함수 gcd가 있다면,
A, B의 최대공약수는 G라는 표현은 아래와 같이 표기 가능합니다.
$ gcd(A, B) = G $
원래의 두 수 A, B는
$ A = a \times G = aG $
$ B = b \times G = bG $
$ A > B $ 일 때,
$ A = BQ + R $
$ R = A - BQ = aG - bGQ = G(a - bQ) $
원래의 두 수 A, B의 최대공약수는,
$ gcd(A, B) = gcd(aG, bG) = G $
작은 수(B)와, 큰 수(A)를 작은 수(B)로 나눈 나머지의 최대공약수로 표현할 수 있습니다.
$ gcd(B, R) = gcd(bG, G(a-bQ)) = G $
아무래도 그림으로 따라가 보는 것이 이해하는데 좋겠군요.
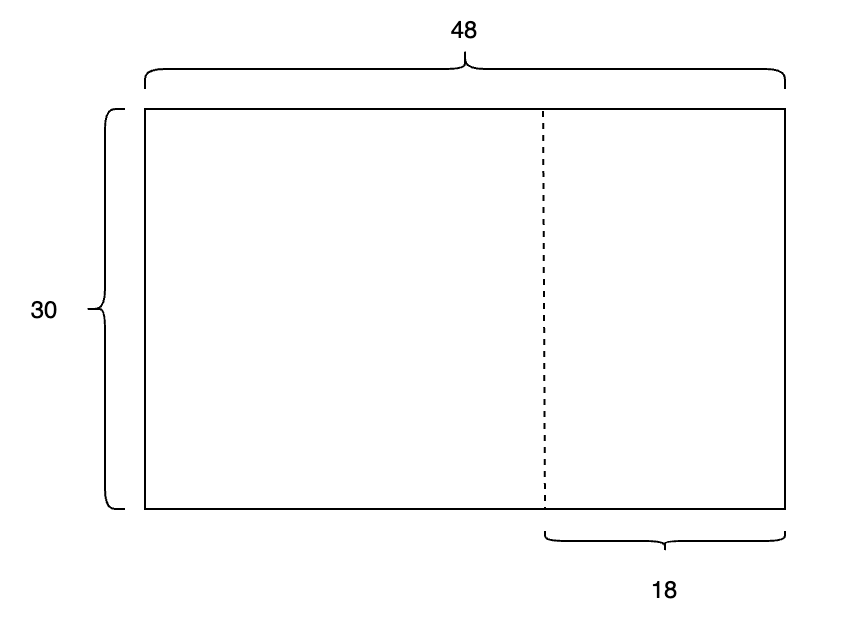
$ 48 = 30 \times 1 + 18 $
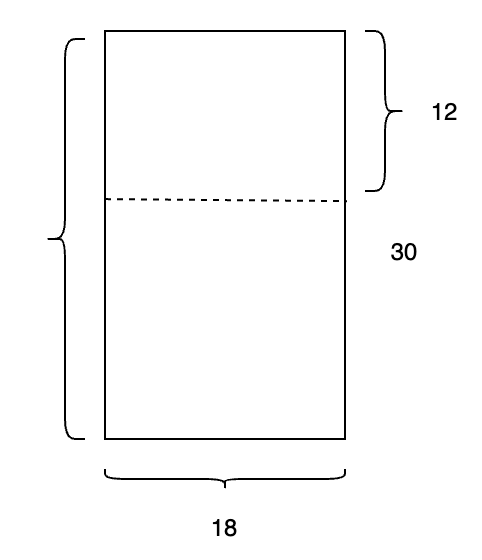
$ 30 = 18 \times 1 + 12 $
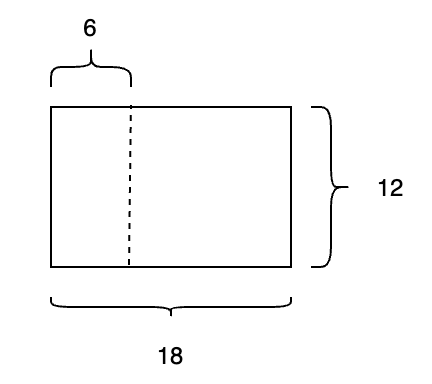
$ 18 = 12 \times 1 + 6 $

$ 12 = 6 \times 2 + 0 $
나머지가 0이 되었으므로, 최대공약수를 찾았습니다.
따라서, 최대공약수는 6이 됩니다.
이상 여러가지 방법으로 최대공약수 구하는법을 정리해봤습니다.
'삶 > 눈높이공부' 카테고리의 다른 글
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |
|---|---|
| 초보자도 이해하기 쉬운 대우명제 (1) | 2021.04.12 |
| 최대공약수와 최소공배수 활용 (1) | 2021.02.10 |
| 최소공배수 구하는 법 - 여러가지 방법 비교 (0) | 2021.02.05 |
| 서로소, 소수 (prime number) - 다시 생각해 봅시다 (0) | 2021.01.27 |
| 곱셈공식 - 그림으로 살펴봐요 (2) | 2020.12.29 |
| 베스킨라빈스게임 이기는 법 (2) | 2020.12.21 |
| 초보자도 이해하기 쉬운 마름모 넓이 공식 (4) | 2020.12.14 |