곱셈공식 - 그림으로 살펴봐요
- 삶/눈높이공부
- 2020. 12. 29.
그냥 무조건 외웠던 곱셈공식. 그림으로 접근하면 다른 관점에서 생각해 볼 수 있습니다.
그림으로 살펴보는 (a + b) x (a + b)
$ (a+b)^2 = (a+b)\times(a+b) = a^2 + 2ab + b^2 $
이것을 그림으로 표현해 보면, 다음과 같습니다.
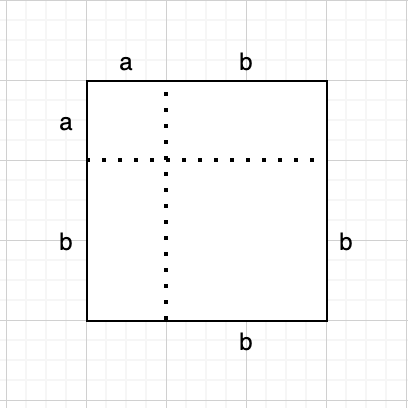
즉, a와 b의 합을 한 변으로 하는 정사각형의 넓이를 구하는 것과 같이 됩니다. 각 구역을 색깔을 입혀보면, 아래와 같이 됩니다.

이 정사각형의 넓이는, 윗쪽의 작은 정사각형의 넓이와 아랫쪽의 큰 정사각형의 넓이, 그리고 두 개의 노란 직사각형의 넓이의 합으로 구성됩니다. 두 개의 노란 직사각형은 서로 넓이가 같습니다.
-
작은 정사각형 넓이 $ s1 = a^2 $
-
큰 정사각형 넓이 $ s2 = b^2 $
-
직사각형 넓이 $ s3 = a \times b $
-
전체 넓이 $ S = (a+b)^2 = s1 + s2 + 2 \times s3 = a^2 + 2ab + b^2 $
그림으로 살펴보는 (a - b ) x (a - b)
$ (a-b)^2 = (a-b)\times(a-b) = a^2 - 2ab + b^2 $
이것을 그림으로 표현해 보면, 다음과 같습니다.

한 변의 길이가 a인 정사각형이 있고, 그 정사각형 속에 작은 정사각형 b가 있는 모습을 상상해 봤습니다. 그러면, 큰 정사각형의 한 변 a = (a - b) + b로 볼 수 있습니다. 다음 그림을 봐주세요.
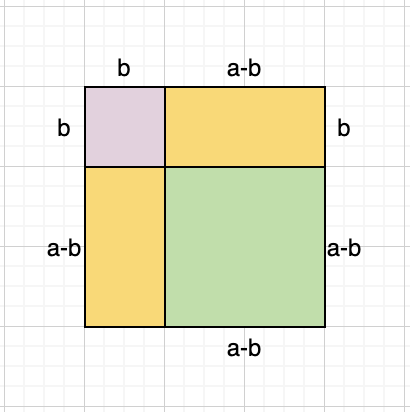
- 초록색 정사각형의 넓이 = 전체 큰 정사각형의 넓이 - 핑크색 작은 정사각형의 넓이 - 노란 직사각형의 넓이(2개)
임을 알 수 있습니다. 위의 문장을 식으로 옮겨보면 다음과 같습니다.
$ (a-b)^2 = a^2 - b^2 - 2 \times (a-b)\times b = a^2 - b^2 - 2ab + 2b^2 = a^2 -2ab + b^2 $
그림으로 살펴보는 (a + b) x (a - b)
$ (a + b) \times (a - b) = a^2 - ab + ba - b^2 = a^2 - b^2 $
사실 수식으로 전개하는 것이 더 쉬워보입니다만, 또다른 어떤 의미가 숨겨져 있는지 그림으로 접근해 보겠습니다.
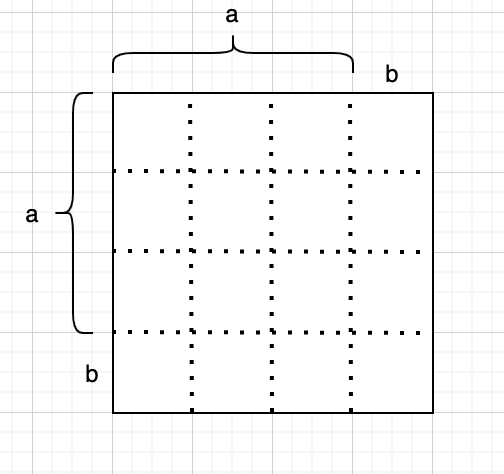
위 그림에서 보듯이 격자를 그려서 보겠습니다. a = 3, b = 1이라고 가정해 보면, a + b = 3 + 1 = 4가 되고, a - b = 3 - 1 = 2가 됩니다. 즉, 다음과 같은 직사각형의 넓이를 구하라는 문제가 되겠군요.

그런데, 이 노란색 직사각형에서 오른쪽 두 칸을 떼어내서 밑으로 옮기면 어떻게 될까요? 다음과 같은 모양이 될 겁니다.
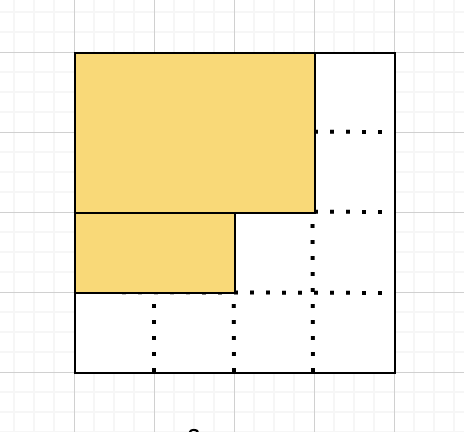
원래 a와 b만 있던 정사각형 모양이 되었군요! 다음의 그림을 보면,

큰 정사각형에서 작은 정사각형의 넓이를 빼는 식으로 적으면 될 것 같습니다.
$ (a + b) \times (a - b) = a^2 - b^2 $
정리
- $ (a+b)^2 = (a+b)\times(a+b) = a^2 + 2ab + b^2 $
- $ (a-b)^2 = (a-b)\times(a-b) = a^2 - 2ab + b^2 $
- $ (a + b) \times (a - b) = a^2 - b^2 $
- 그림으로 생각해 보면 이해하는데 도움이 됩니다.
'삶 > 눈높이공부' 카테고리의 다른 글
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |
|---|---|
| 초보자도 이해하기 쉬운 대우명제 (1) | 2021.04.12 |
| 최대공약수와 최소공배수 활용 (1) | 2021.02.10 |
| 최소공배수 구하는 법 - 여러가지 방법 비교 (0) | 2021.02.05 |
| 최대공약수 구하는법 - 여러가지 방법 비교 (3) | 2021.02.03 |
| 서로소, 소수 (prime number) - 다시 생각해 봅시다 (0) | 2021.01.27 |
| 베스킨라빈스게임 이기는 법 (2) | 2020.12.21 |
| 초보자도 이해하기 쉬운 마름모 넓이 공식 (4) | 2020.12.14 |