원의 둘레 공식, 원의 넓이 공식 이해하기
- 삶/눈높이공부
- 2023. 1. 16.
원의 둘레 공식, 원의 넓이 공식 이해하기
우리는 원의 둘레 공식과 원의 넓이 공식에 대해 일단 외우기 부터 했습니다.
그러나, 단순하게 외우기만 해서는 오래 기억에 남지 않겠죠.
그 특징을 이해해 보고 넘어가야 합니다.
원의 특성
먼저 원에 대해 생각해 보죠.
일상에서 많이 접하는 원, 그런데 원의 정의에 대해서 생각해 본적이 있나요?
원은 어떤 한 점을 기준으로 선을 그을 때, 한 점과 같은 거리에 있는 점들의 집합입니다.
콤파스를 써봤다면 이해하기 쉬울텐데, 몇 cm 짜리 길이를 정한 후, 돌린다면 원이 나오죠.
같은 길이만큼 떨어져 있는 점들의 집합이 원입니다.
원의 둘레 공식
중심의 한 점으로부터 같은 거리에 있는 점들을 이어 선을 이으면 원이 된다고 했죠?
그러면, 선을 긋는 시작점이 있을 것입니다.
그리고 시작점으로부터 선을 긋기 시작해서 한바퀴 돌고 다시 제자리에 오면 선 긋기가 완료되고, 그 시점에 원이 완성이 됩니다.
시작점으로부터 끝점까지 선을 그어서 이동한 거리가 얼마나 될까를 옛날사람들도 많이 궁금해 했습니다.
끝내 어떤 규칙을 발견했냐하면, 원의 둘레의 길이는 지름의 약 3배 정도 된다는 내용이었습니다.
게다가 이 규칙은 원의 크기와는 관계없이 일정한 비율이 보장된다는 것 또한 발견했습니다.
이 비율의 값은
3.14159265358979323846264338327950288419716939937510582097494459230781.....
입니다.
매번 저렇게 긴 값을 쓸 수도 없고, 자릿수가 무한하게 커치므로 저 값을 파이($ \pi $)로 부르기로 했습니다.
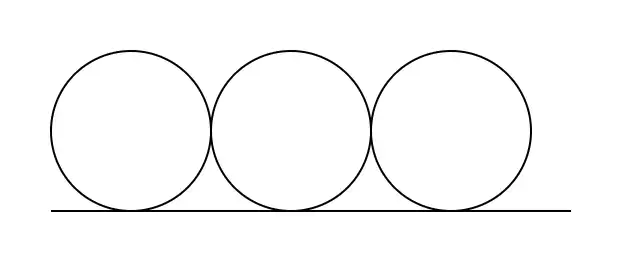
둘레의 길이는 지름의 길이의 $ \pi $ 배가 된다는 것을 공식으로 옮기면 아래와 같습니다.
$ l = D \times \pi $ (단, D = 지름)
$ l = 2 \times r \times \pi $ (단, r = 반지름)
$ l = 2 \times \pi \times r $
원의 넓이 공식
원의 넓이는 어떻게 구할까요?
우리에게 익숙한 원인 피자로 넓이를 구하는 방법을 생각해 봅시다.
피자를 보통 8조각으로 쪼개는데, 이 조각을 더 잘게 쪼개봅시다.
크러스트 부분이 거의 직선에 가까워지도록.
그리고, 이렇게 쪼갠 것을 한 쌍으로 묶으면 거의 사각형에 가깝게 만들 수 있을 것입니다.
한 조각은 뾰족한 부분이 위를 바라보게 하고, 다른 한 조각은 뾰족한 부분이 아래를 바라보게 합니다.
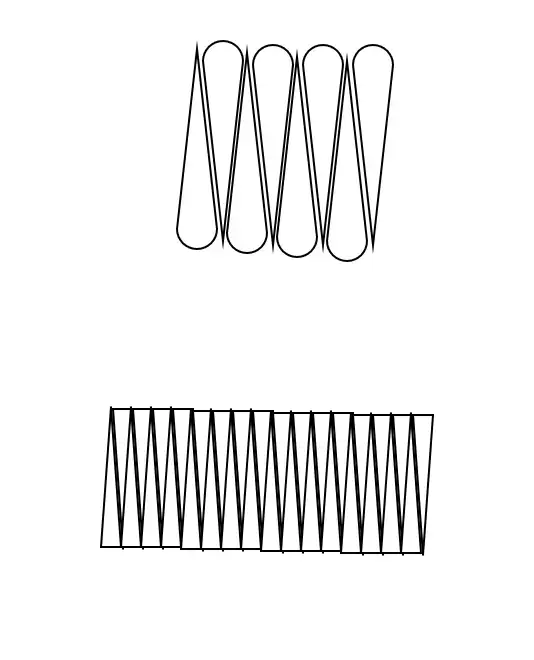
크러스트 부분이 짧으면 짤을수록 이 쌍은 사각형의 모양에 가까워집니다.
이렇게 피자를 재조합하고 나면, 전체 모양이 원에서 직사각형으로 바뀌는 것을 확인할 수 있습니다.
직사각형 넓이는 쉽게 구할 수 있죠.
가로 곱하기 세로입니다.
세로는 피자의 반지름 r이 되고, 가로는 피자를 재조합해서 만든 크러스트 부분이되겠네요.
위에서 원의 둘레는 $ l = 2 \times \pi \times r $ 이라고 했습니다.
그런데 사각형으로 만들어 놓고 보니, 상단의 선과 하단의 선을 합치면 원의 둘레가 됩니다.
즉, 사각형 모양으로만 보자면, 원의 둘레의 반이 직사각형에서의 가로 길이 부분이 됩니다.
이제 사각형의 넓이를 구할 수 있겠네요.
- 가로 = $ \pi r $
- 세로 = $ r $
따라서, 두 값을 곱한 값이 곧 원의 넓이가 됩니다.
$ S = \pi \times r^2 $
더 보기
'삶 > 눈높이공부' 카테고리의 다른 글
| 원기둥 부피 공식 이해하기 (0) | 2023.02.18 |
|---|---|
| 두 분수에 곱해서 자연수를 만들 수 있는 가장 작은 분수 구하기 (0) | 2022.05.16 |
| 근의 공식 유도 (0) | 2021.07.22 |
| 피타고라스정리 - 닮은 삼각형으로 증명 (0) | 2021.07.07 |
| 피타고라스 정리 - 유클리드 증명 (0) | 2021.06.30 |
| 피타고라스 정리 - 가필드식 증명 (0) | 2021.06.23 |
| 피타고라스 정리 - 바스카라식 증명 (0) | 2021.06.16 |
| 피타고라스 정리 - 피타고라스식 증명 (0) | 2021.06.09 |